Se denomina catenaria la curva que describe una cadena suspendida entre dos puntos situados a la misma altura. Por ejemplo se llaman catenarias a los cables del tendido eléctrico de los ferrocarriles, no por el cable conductor de la electricidad, sino por el cable superior que le sustenta entre dos postes del tendido. La catenaria tiene la característica de ser el lugar geométrico de los puntos donde las tensiones horizontales de un cable se compensan por lo que el cable no tiene tensiones laterales, el cable no se desplaza hacia los lados y a las fuerzas que padece se reparte entre una fuerza vertical (la de la atracción terrestre) y una tensión tangente al cable en cada punto que lo mantiene estirado..

De igual forma, en un arco que adquiera la forma de una catenaria, la tensión que padece el arco en cada punto, se reparte entre una componente vertical que será lo que tenga que sustentar el propio arco y una componente de presión que se transmite por el propio arco hacia los cimientos sin que se creen esfuerzos horizontales, salvo en el extremo llegando ya a los cimientos.

Esta propiedad, distintiva y única de este tipo de arcos, hace que no necesiten apoyo a los lados del arco para sustentarse y evitan que tiendan a abrirse. En las capillas románicas eran necesarios gruesos muros a los lados de puertas y ventanas para mantener los arcos de medio punto sin que se agrietara. Tampoco los arquitectos medievales consiguieron encontrar la forma perfecta de transmitir los esfuerzos laterales y pese a que los arcos ojivales se aproximan más a la forma de la catenaria, aun necesitaron apoyar sus arcos en fuertes arbotantes exteriores que absorbían y trasladaban las tensiones horizontales hacia los cimientos.

Los arquitectos del renacimiento tampoco supieron encontrar la solución, La cúpula de San Pedro, diseñada por Miquel Ángel, está rodeada en su base por una fuerte cadena de hierro a modo de cincha, porque una vez construida comenzó a agrietarse debido a estas fuerzas horizontales creadas por el peso de la cúpula.

Tenemos que llegar al modernismo del siglo XIX para que arquitectos como Gaudí recapaciten que no necesariamente las líneas verticales absorben mejor las tensiones. Muchas de sus obras, desde la Sagrada Familia, a la casa Batlló, la Pedrera, o el parque Guell, enseñan en las fachadas o ocultan en sus sótanos o en sus azoteas, arcos de catenaria que desvían el peso de las cubiertas dejando amplias zonas abiertas..

Otro arquitecto catalán como Gaudí y contemporaneo suyo, participa de las mismas inquietudes, y es difícil saber cual de los dos influyo en el otro. Se trata de Luis Mancunill, arquitecto más desconocido del público, pues el resplandor de la figura de Gaudí, ensombrece la de otros arquitectos modernistas y además gran parte de su obra se desarrollo en Tarrassa y en a la construcción de centros fabriles, ciudad y obra menos atractiva para los críticos que Barcelona y los palacetes y templos. De él es el edificio que abre el artículo la Masía Freixa, una joya del Modernismo construida en 1896 como fábrica y transformada en residencia de la familia Freixa en 1907.

Lo que parecen caprichos y arabescos de un arquitecto barroco con arcos extraños y columnas torcidas, ocultan concienzudos estudios en la búsqueda de la forma más racionalistas para las estructuras de sus edificios.

Se conserva una fotografía del estudio que hizo Gaudí para diseñar la Capilla de la Colonia Guell. Con gran paciencia fue realizando con cadenas una copia invertida a escala 1/10 de la visión que el tenía de lo que el quería construir. A la estructura inicial fue añadiendo pequeñas cadenas con pesos proporcionales a los torreones que el deseaba que decoraran el edificio. El resultado obtenido lo fotografiaba y a partir de las fotografías diseñaba los planos de construcción, resulta curioso comparar el estudio con el boceto de la capilla pintado por Gaudí.

Rotos los prejuicios, otros arquitectos han utilizado el arco catenario en sus edificaciones. Calatrava lo utiliza abundantemente en sus edificios de la Ciudad de las Artes y las Letras de Valencia, así como en numerosísimos puentes. Así como es muy conocido el arco que de una forma simbólica marca la puerta de la “Conquista del Oeste” el Gatewey Arch de la ciudad de Missouri, de 192 m. de altura del arquitecto Eero Saatinen.

Lo que en Occidente nos ha costado siglos aprender, era en cambo un conocimiento común en la arquitectura del Islam. la cúpula Mezquita de la Roca de Jerusalén se aproxima mucho a una cúpula catenaria perfecta.

En esto no hacían más que seguir la arquitectura tradicional del Sudán, país donde la madera es tan escasa y valiosa, que no se puede utilizar para construir las viviendas de los pobres. Los sudaneses encontraron la forma de construir amplias habitaciones circulares con forma de cúpula catenaria, con solo adobe y sin necesidad de entibar, pues durante el momento de la construcción sufre tan poco empuje horizontal, que los adobes se mantienen en su posición simplemente con el rozamiento de los ya instalados y sus compañeros de hilada y una vez cerrada la cúpula, estas adquieren una resistenxia extraordinaria.

Se cierra así una práctica que une lo mas ancestral, con lo más moderno. Las centrales nucleares suelen cubrir el reactor con una cúpula catenaria por la misma razón, la posibilidad de construirlas sin andamiaje que la sustente.

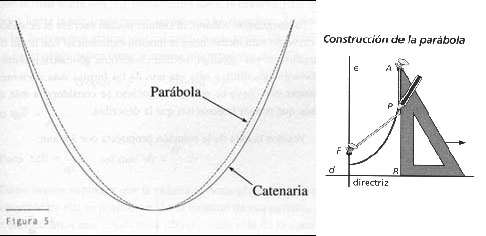El desarrollo de la fórmula matemática de la curva catenaria es sus tres primeros términos de potencia es igual al de una parábola (y = a+ bx+ cx2) y solo a partir de aquí difiere con términos de potencia de x elevados a 4 o más, por ello, catenaria y parábola difieren poco en valores bajos de x, es decir cerca del «morro» de la curva. La diferencia fundamental es que al tangente de la curva, en la parábola tiende hacia un valor fijo, mientras que en la catenaria tienden hacia la posición vertical. Ello lleva a que a medida que crece la x sus curvas se cruzan y mientras la catenaria tiende a valores limitados de x, la parábola se abre indefinidamente hasta el infinito.

Esta propiedad es útil pues construir arcos parabólicos en vez de arcos de catenaria, es más sencillo, pues mientras que la curva catenaria es difícil de pintar y calcular, la parábola se puede puntar a escala con solo la ayuda de una escuadra tan alta como la parábola a pintar, un papel milimetrado, una regla para deslizar la escuadra, un hilo y un par de chinchetas puestas en el foco y en el borde de la escuadra que sujetan la cuerda tal como se ve en la figura, se aprovecha para ello de la propiedad de la parábola de ser el lugar geomético de los puntos cuya suma de distancias a a otros dos es fijo , (la longitud del hilo). Solo basta hacer la parábola a escala y medir las distancias a cada diferente nivel de la curva.

.